कक्षा 11, अर्थशास्त्र- आँकड़ों का प्रस्तुतीकरण पुनरावृत्ति नोट्स यहां पढ़ें।
CBSE और उत्तराखंड बोर्ड, कक्षा 11 अर्थशास्त्र
पाठ - 4 आँकड़ों का प्रस्तुतीकरण
पुनरावृत्ति नोट्स
स्मरणीय बिन्दु-
- सामान्यतः आँकड़े जटिल होते हैं अतः उन्हें स्पष्ट एवं व्यवस्थित रुप में प्रस्तुत करना आवश्यक होता है। आँकड़ों के प्रस्तुतीकरण की तीन विधियां-
- सारणीयन प्रस्तुतीकरण
- चित्रमय प्रस्तुतीकरण
- ग्राफीय प्रस्तुतीकरण
- सारणीयन प्रस्तुतीकरण-इसमें आँकड़ों को स्तम्भों तथा पंक्तियों के रुप में प्रस्तुत किया जाता है। इस विधि का प्रमुख लाभ यह है कि यह आँकड़ों को पुनः सांख्यिकीय व्यवहार तथा निर्णय प्रक्रिया के लिए व्यवस्थित करता है।सारणी निर्माण के लिए आवश्यक है कि अच्छी सारणी के भागों को जाना जाये जिसके व्यवस्थित क्रमबद्ध तरीके से सारणी का निर्माण हो सके। सारणी निर्माण की सबसे सरल प्रक्रिया आँकड़ों का स्तम्भों और पंक्तियों में कुछ व्याख्यात्मक नोट के साथ प्रस्तुत करना है।गुणों की संख्या के आधार पर एक गुणी, द्विगुणी और बहुगुणी वर्गीकरण का उपयोग सारणीयन में किया जा सकता है। एक अच्छी सारणी द्विगुणी में निम्न आवश्यक है-
- सारणी संख्या
- शीर्षक
- स्तम्भ शीर्षक (Caption)
- पंक्ति शीर्षक (Row)
- सारणी का आकार
- मापन की इकाई
- स्रोत नोट
- फुटनोट (Footnote)सारणी संख्याशीर्षक ........(शीर्ष नोट) ........
पंक्ति शीर्षक | स्तम्भ | कुल (पंक्ति) | |
|
|
|
|
कुल (स्तम्भ) |
|
|
|
स्रोत नोट ..........
फुट नोट ...........
- चित्रीय प्रस्तुतीकरण- इस विधि में पाठ्य तथा सारणीपन प्रस्तुतीकरण कि तुलना में आँकड़ों के द्वारा आँकड़ों का प्रभावपूर्ण और काल्पनिक तथा तुलनात्मक अध्ययन आसान हो जाता है।चित्र सारणी की तुलना में कम या अधिक शुद्ध प्रस्तुतीकरण कर सकता है। सामान्य प्रयोग में प्रस्तुतीकरण के कई प्रकार है उनमें कुछ महत्वपूर्ण निम्न है –
- ज्यामितीय चित्र
- आवृत्ति चित्र
- रेखीय ग्राफ
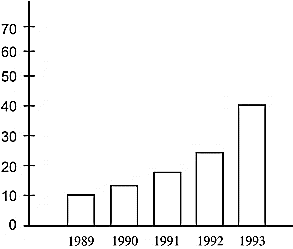
- ज्यामितीय चित्र- इस श्रेणी में दण्ड आरेख तथा वृत्तीय आरेख आते हैं।दण्ड आरेख- दण्ड आरेख प्रत्येक वर्ग के आँकड़ों के लिये आयताकार दण्ड का समूह है। दण्ड की ऊँचाई या लम्बाई आँकड़े के परिमाण पर निर्भर करती है दण्ड आरेख के दण्ड को देखकर उनकी सापेक्षिक ऊँचाई के आधार पर आँकड़ों का तीव्रतर तुलना की जा सकती है।उदाहरण-
Year | 1989 | 1990 | 1991 | 1992 | 1993 |
Profit | 10 | 12 | 18 | 25 | 42 |
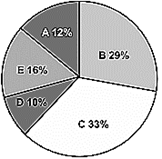
- वृत्तीय चित्र-यह एक घटक चित्र है जिसमें वृत्त का क्षेत्र आनुपातिक रुप से प्रस्तुत घटकों के मध्य विभाजित होता है। इसे पाई चार्ट, वृत्तीय आरेख, पिज्जा चार्ट और सेक्टर आरेख भी कहा जाता है।वृत्त घटकों के अनुसार विभिन्न भागों में विभाजित होता है तथा प्रत्येक विभाजन के लिए वृत्त के केन्द्र से परिधि तक सीधी रेखा खींची जाती है।
- वृत्तीय चित्र वर्ग के निरपेक्ष मूल्य से नहीं बनाया जाता है। प्रत्येक वर्ग का मूल्य कुल मूल्य के प्रतिशत में प्रस्तुत किया जाता है।
- वृत्त को 3.6० (360/100) के 100 समान भागो में बाँटा जा सकता है। प्रत्येक घटक कोणीय मान को वृत्त में प्रस्तुत करने के लिए उसके प्रतिशत भाग को 3.6० से गुणा कर के प्राप्त किया जाता है।
- यह जानना रुचिपूर्ण है कि आँकड़ों के द्वारा प्रदर्शित घटकों को ठीक-ठीक वृत्त में दर्शाया जा सकता है। इसकी सममात्र आवश्यक शर्त है कि उनके निरपेक्ष मूल्य को प्रतिशत मूल्य में बदलने के उपरान्त ही वृत्तीय आरेख में उपयोग किया जाये।
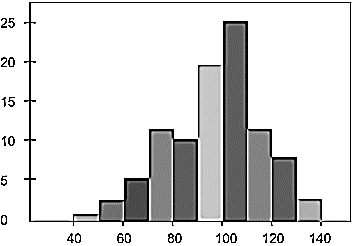
- ग्राफीय प्रस्तुतीकरणआवृत्ति चित्र– सामूहिक आवृत्ति वितरण के रुप में आँकड़े सामायत आवृत्ति चित्रों जैसे आयत चित्र, बहुभुज तथा ओजाइव वक्र के रुप में प्रस्तुत किए जाते हैं।आयत चित्र- यह एक द्विवीमिप चित्र है। इसमें वर्ग अन्तराल तथा उनकी आवृत्तियों को आयत के रुप में प्रस्तुत करके बनाया जाता है।
- आँकड़ों को आयत चित्र में प्रस्तुत करने के लिए आयत की ऊँचाई (आवृत्ति) और आधार (वर्ग अन्तराल) होता है।
- खण्डित चर के लिए आयत चित्र सम्भव नही है।
- यदि वर्ग सतत नही है तो पहले उन्हे सतत वर्ग में परिवर्तित किया जाता है।
- आयत चित्र में दो आयत के मध्य कोई रिक्तता नहीं रहती जबकि दण्ड आरेख में ऐसा होता है।
- दण्ड आरेख में आयत की चौड़ाई महत्वपूर्ण नही होती जबकि आयत चित्र में ऊचाई के साथ-साथ चौड़ाई भी महत्वपूर्ण होती है।
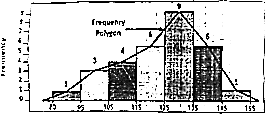
- बहुभुज- आवृत्ति बहुभुज चार या चार से अधिक रेखाओं से घिरी हुई होती है। यह आयत चित्र का विकल्प है और आयत चित्र से ही प्राप्त किया जाता है। एक आवृत्ति बहुभुज आयतचित्र के अनुरुप बनाया गया वक्र है। इसे बनाने की सबसे सामान्य विधि है- आयतचित्र के शीर्ष मध्य बिन्दुओं को सरल रेखा द्वारा मिलाते हुए दोनों सिरों को बढ़ाकर आधार रेखा तक बन्द कर दिया जाता है।
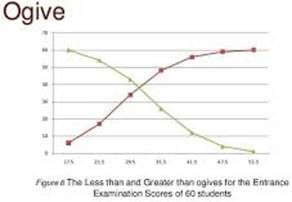
- ओजाइव या संचयी आवृत्ति वक्र- ओजाइव को संचयी आवृत्ति वक्र भी कहते हैं। जैसा कि संचयी आवृत्ति के दो प्रकार (से कम) या (से अधिक) होते हैं। अतः हमारे पास दो प्रकार की संचयी आवृत्ति वक्र है। आवृत्ति बहुभुज की तुलना में इसमें y-अक्ष पर संचयी आवृत्ति को दर्शाया जाता है। तथा x - अक्ष पर वर्ग-अंतराल को। “से कम” विधि में वर्ग आवृत्ति में पिछले वर्ग अंतराल की आवृत्तियों को जोड़ा जाता है जबकि “से अधिक” में घटाया जाता है। इस प्रकार अनुरुप वर्ग अंतराल की ऊपरी और निम्न सीमा के अनुसार अंकित करते हैं तथा प्राप्त बिन्दुओ को मुक्त हस्त से मिला दिया जाता है। दो संचयी आवृत्ति वक्रों की विशिष्ट विशेषता होती है कि इनका प्रतिच्छेदन पद माध्यिका का मूल्य प्रदान करता है।
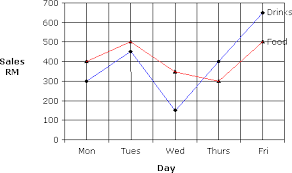
- कालिक श्रृंखला ग्राफ या रेखीय ग्राफ- आँकड़ों के चित्रीय प्रस्तुतीकरण की रेखीय ग्राफ विधि को कालिक श्रृंखला ग्राफ विधि भी कहा जाता है। इसमें समय (घंटा, मिनट, सेकण्ड, दिन, महीना, वर्ष इत्यादि) को x-अक्ष पर अंकित किया जाता है तथा आश्रित चर को Y अक्ष पर अंकित किया जाता है तथा आश्रित चर को Y-अक्ष पर अंकित किया जाता है। इस प्रकार प्राप्त इन बिन्दुओं को सरल रेखा से मिलाने पर रेखीय ग्राफ प्राप्त किया जाता है। यह सामयिक चलन (ट्रेड) को समझने में सहायक है।

.jpeg)

.jpeg)

.jpeg)




.jpeg)
Comments
Post a Comment
पोस्ट पर अपने उपयोगी विचार और सुझाव यहाँ कमेंट करें।